The Math of Games: What Is Transitivity in Game Theory?
I know it’s called Math of Games, but I promise it’s the fun kind of math! I also promise that “fun math” is a real thing.
For long time readers, you may remember I used to dive into some of the mechanics of games. It was a series looking at various game mechanics. First, we’d look at the mechanic itself, and break it down to better understand it. Then we’d look at some games which used the mechanics well, then finally we designed our own game using the mechanic.
I’m still salty no one appreciated my poorly photoshopped ‘deck builder’ joke picture
As you might expect from my doing all that, I enjoy looking at games scientifically and mathematically in a branch of math called Game Theory.
I do like the channel, but not what we’re talking about here.
Game Theory is looking at games logically, in the literal sense. It’s the branch of math that asks “If you have to choose between A and B, which should you choose?”. It’s the branch of math which determines you should always switch doors in the Monty Hall problem.
Transitivity
Like explaining why a joke is funny, let’s analyze games to the point of ruining their fun by taking a look at a concept called Transitivity.
You may remember from middle school math the idea of the Transitive Property. The idea is that if A = B and if B = C then A = C. The properties of A transit down the chain of equality to C. This concept can apply to games as well. But in our case, the A, B, and C are gameplay strategies. If strategy A is preferable to strategy B, and strategy B is preferable to strategy C, then strategy A is preferable to B and to C. Making it the best strategy.
For gameplay balance, this might seem like a bad thing. A singular optimal strategy takes away replayability if you just do the same thing over and over and always win, right? So what’s the best way to fix that?
Non-Transitive Games
You already know the answer, even if you don’t realize it just yet.
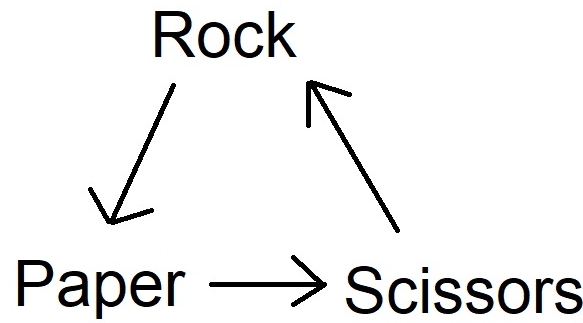
Rock, Paper, Scissors is the quintessential non-transitive game.
Notice the loop of a non-transitive game. This loop is what makes it non-transitive, because that forces there to be no best strategy or move. Non-transitive games usually have things like multiple unit options. Like Cavalry beat Infantry, Infantry Beat Spearmen, but Spearmen beat Cavalry.
If non-transitive games give no best strategy, that means more viable strategies, meaning more viable gameplay options, which is good, right? So why aren’t all games non-transitive?
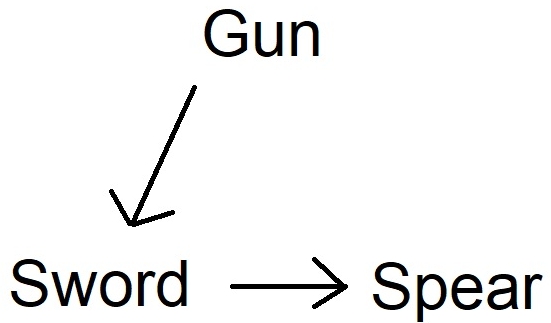
Transitive Games
Look back to our diagram for transitive games. Gun beats sword beats spear.
Well, okay, but MOST of the time it’s true.
Memes aside, transitive games usually have elements of leveling up and upgrading. Adamantine beats Steel, Steel beats Copper, Copper sucks and doesn’t beat anything.
Which is best?
It should come as no surprise there’s no best option. The decision of transitive vs non-transitive is, itself, non-transitive.
It comes down to what sort of game you’re playing. And games can even have elements of both. Boss beats Nob who beat Boy who beat Grot.
That’s transitive. But the points system and battle detachment system prevent players from just taking an army of Ork Bosses, even though that should be an “optimal strategy”.
However, in the decision between Orks and Marines, or Orks and Eldar, and Orks or Tyranid…
OF CORSE YA PICK ORKS. CUZ ORKS IS MADE TA FIGHT AN’ TA WIN! ORKS NEVER LOSE! WAAAGH!
FANKS FOR REEDIN’!
